From Chaos to Clarity: The Philosophy and Mathematics of Gaussian Noise

Introduction: The Hidden Image
Imagine a sculptor standing before a raw block of marble. The stone is a chaotic mass of potential, but within it, the sculptor envisions a finished form. Their job is not to create something from nothing, but to chip away the excess—the “noise”—to reveal the sculpture that was always latent within.
What if we could do the same with a digital canvas? What if, instead of starting with a blank slate, we started with pure, unstructured chaos and, like a sculptor, systematically removed the noise to reveal a breathtaking image?
This is the profound idea at the heart of modern generative AI. These models challenge our traditional view of creation and perfection. They suggest that every image is essentially a form of organized noise, and that art emerges from finding the perfect balance between chaos and clarity. In this post, we’ll explore this fascinating intersection of philosophy, mathematics, and artificial intelligence, starting with the raw material of creation itself: Gaussian noise.
The Universal Analogies: Creation from Chaos
To understand how an AI can “sculpt” an image from noise, it helps to look at timeless creative processes.
- The Sculptor’s Touch: Revealing Perfection by “Denoising” A block of stone is like a canvas of raw Gaussian noise—full of potential but lacking structure. The sculptor’s chisel is a tool of “denoising,” iteratively removing irrelevant material to bring the hidden form into focus. This mirrors how an AI image generator works. Guided by a text prompt (the sculptor’s vision), the model progressively refines a noisy canvas, with each pass chipping away at the “wrong” pixels until the desired image emerges.
Philosophically, the sculpture was always “there,” waiting to be uncovered. Similarly, the AI assumes the perfect image is latent within the noise, and its role is to find it.
From Art to Data: An Image is a Matrix
At its core, a digital image is not inherently visual; it’s a mathematical abstraction.
Pixels and Values: An image is a grid of pixels. In a grayscale image, each pixel has a single brightness value (e.g., 0 for black, 255 for white). In a color (RGB) image, each pixel has three values for red, green, and blue.
Matrix Representation: This grid of values can be represented as a matrix. A grayscale image is a 2D matrix, while a color image is a 3D matrix.
An image is represented as a matrix of pixel intensity values:
$$ \text{Image} = \begin{bmatrix} I_{1,1} & I_{1,2} & I_{1,3} & \cdots & I_{1,n} \\ I_{2,1} & I_{2,2} & I_{2,3} & \cdots & I_{2,n} \\ I_{3,1} & I_{3,2} & I_{3,3} & \cdots & I_{3,n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ I_{m,1} & I_{m,2} & I_{m,3} & \cdots & I_{m,n} \\ \end{bmatrix} $$Every operation—applying a filter, resizing, or AI generation—is a mathematical manipulation of this matrix. This is the paradox: every digital image, no matter how beautiful, is fundamentally a structured arrangement of numerical noise.
The Mathematics of Creative Chaos: Gaussian Noise
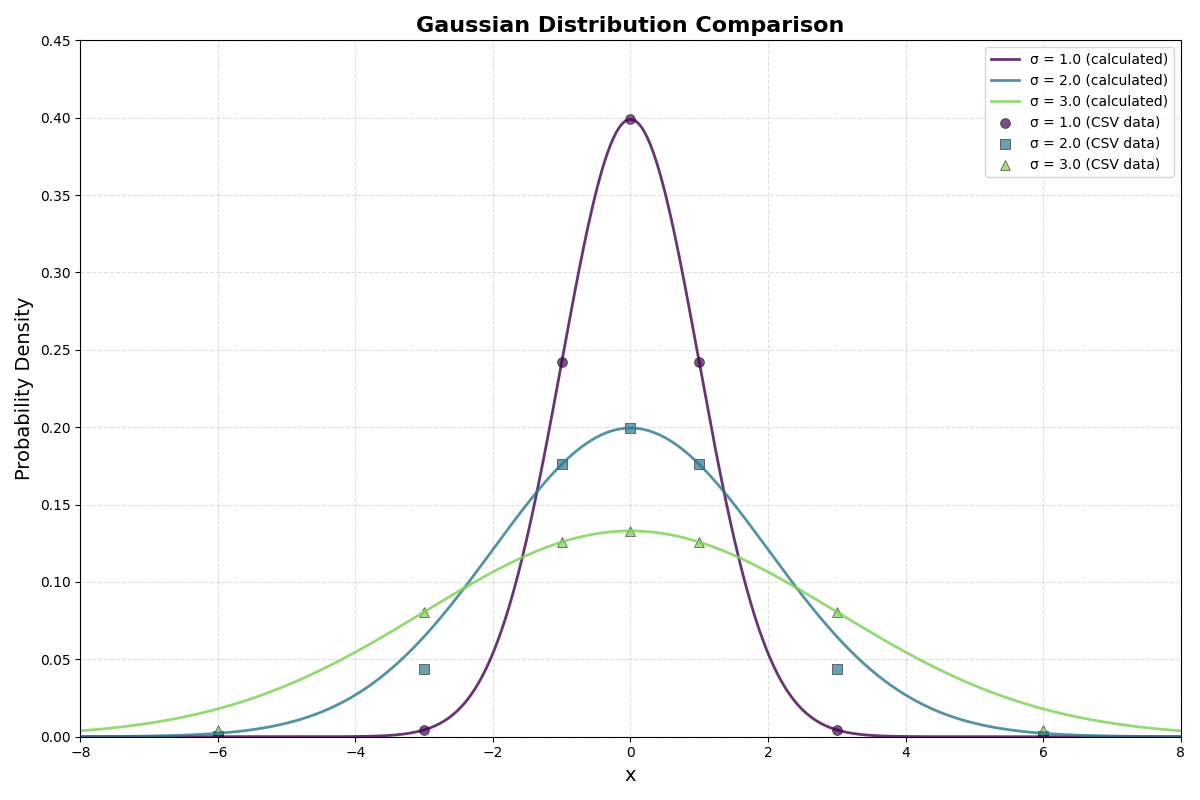
Generative models need a specific kind of chaos to work with, and they most often use Gaussian noise. This is because its properties are predictable and mathematically elegant. It is defined by the Gaussian (or normal) distribution, a bell-shaped curve described by this formula:
Gaussian distribution: \(P(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}\)
Let’s break this down:
P(x) is the probability of a certain value occurring.
μ (mu) is the mean, or the center of the peak. In image noise, this is often 0.
σ (sigma) is the standard deviation, which controls the “spread” of the bell curve. A low σ means most values are clustered around the mean (less noisy), while a high σ means values are spread out (more noisy).
Gaussian noise is used in diffusion models because it’s simple, universal, and allows for the smooth, gradual transitions needed to “sculpt” an image.
The “Random Number Picker” Process
Here’s a step-by-step breakdown of how the AI uses the distribution to generate this initial noise:
Prepare the Canvas: The AI starts with a blank digital canvas, which is essentially a grid of pixels. For a color image, every single pixel has three channels: Red, Green, and Blue (RGB).
“Roll the Dice” for Every Channel: For each pixel, the AI needs to assign a random value to its Red channel, its Green channel, and its Blue channel. It “rolls the dice” for each of these using the Gaussian distribution as its guide.
Picking the Values: The bell curve dictates that values near the mean (center) are the most likely to be picked. This means most of the randomly generated numbers will be moderate, resulting in shades of gray. Occasionally, the “dice roll” will land further from the center, picking a higher or lower value and creating a much brighter or darker spot.
The result of this process is a canvas filled with what looks like natural, non-uniform static. This noise is not completely random; it’s structured chaos that follows the statistical rules of the Gaussian distribution. This “noise canvas” is the perfect starting point for the AI to begin its denoising process and sculpt a coherent image.
For a color (RGB) image, the AI “rolls the dice” three separate times for each individual pixel:
Once for the Red channel.
Once for the Green channel.
Once for the Blue channel.
Each channel gets its own independent random value drawn from the Gaussian distribution. Combining these three random values gives a single pixel its specific, random color in the initial noise field. This entire three-roll process is then repeated for every pixel on the canvas.
Say, for example, the values below:
| x Value | PDF (σ=1.0) | PDF (σ=2.0) | PDF (σ=3.0) |
|---|---|---|---|
| -6 | 0.000001 | 0.000487 | 0.004432 |
| -3 | 0.004432 | 0.043939 | 0.080657 |
| -1 | 0.241971 | 0.176033 | 0.125794 |
| 0 | 0.398942 | 0.199471 | 0.132981 |
| 1 | 0.241971 | 0.176033 | 0.125794 |
| 3 | 0.004432 | 0.043939 | 0.080657 |
| 6 | 0.000001 | 0.000487 | 0.004432 |
would generate these curve below. These values can be used to come up with the values for each channel in the RGB.
How Diffusion Models Sculpt Noise
Now, let’s connect the mathematics to the practical workings of a model like Stable Diffusion. The process is a beautiful dance between adding and removing noise.
Forward Diffusion (The Training): In the training phase, the model learns about noise. It takes a massive dataset of real images and intentionally corrupts them by gradually adding layers of Gaussian noise until nothing is left but a chaotic field of static. The model’s goal is to learn how to reverse this process.
Reverse Diffusion (The Creation): This is where the magic happens.
The process starts with a brand-new, randomly generated canvas of pure Gaussian noise.
Guided by a text prompt (e.g., “an astronaut riding a horse”), the model begins the denoising process.
Step-by-step, it predicts what a slightly less noisy version of the image would look like and subtracts that predicted noise. The architecture often used for this is a U-Net, which is excellent at processing images at different scales.
With each iteration, the model refines the image, moving from total chaos to a coherent picture that matches the prompt. The attention mechanisms within the model help it focus on the right parts of the image to ensure, for instance, that the astronaut is on the horse, not next to it.
[Suggestion: Include a visual diagram showing the progression from pure noise to a finished image over several steps of the reverse diffusion process.]
Philosophy of Perfection: Wabi-Sabi and Balanced Noise
The traditional Western view of perfection is often one of flawlessness and absolute symmetry. But generative AI aligns more closely with philosophies that find beauty in imperfection, like the Japanese concept of wabi-sabi. Wabi-sabi appreciates the texture, asymmetry, and “flaws” that make things authentic and unique.
This leads to our central thesis: Perfection is not the absence of noise, but noise that is controlled and proportionate to the desired outcome.
Real-world images are never flawless. They contain film grain, sensor noise, the unpredictable patterns of light on water, or the chaotic arrangement of leaves in a forest. It is this blend of order and randomness that makes them feel real and compelling. Generative models embrace this by using noise as a creative medium, allowing for infinite variation and serendipitous discoveries.
Conclusion: The Harmony of Chaos and Order
We began with a block of marble and ended with the mathematics of generative AI. Along the way, we’ve seen that the creation of an image—whether by a sculptor, a musician, or an algorithm—is an act of transforming chaos into meaning.
AI art teaches us to redefine perfection. It’s not about eliminating every imperfection but about finding the beautiful harmony between randomness and structure. The noise is not a flaw to be removed, but the very canvas from which creativity emerges. As we continue to develop these powerful tools, we are reminded that in art, as in life, the most beautiful outcomes arise from finding the perfect, delicate balance between chaos and order.